Triangolo rettangolo: caratteristiche e formule

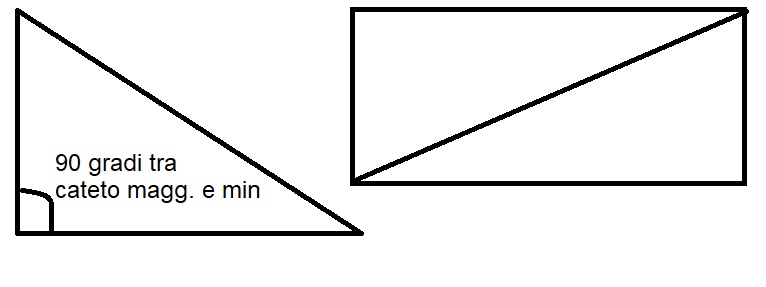
Il triangolo rettangolo ha come caratteristica principale l’angolo di 90 gradi formato dai due lati chiamati cateto maggiore e cateto minore.

Se fosse costruito un triangolo rettangolo uguale e attaccato all’ipotenusa ne verrebbe fuori un rettangolo o un quadrato. Prima di passare alle formule del perimetro e dell’area vediamo bene da cosa è composta la figura che stiamo studiando e altre sue caratteristiche.

Triangolo rettangolo: cateti, altezza e ipotenusa

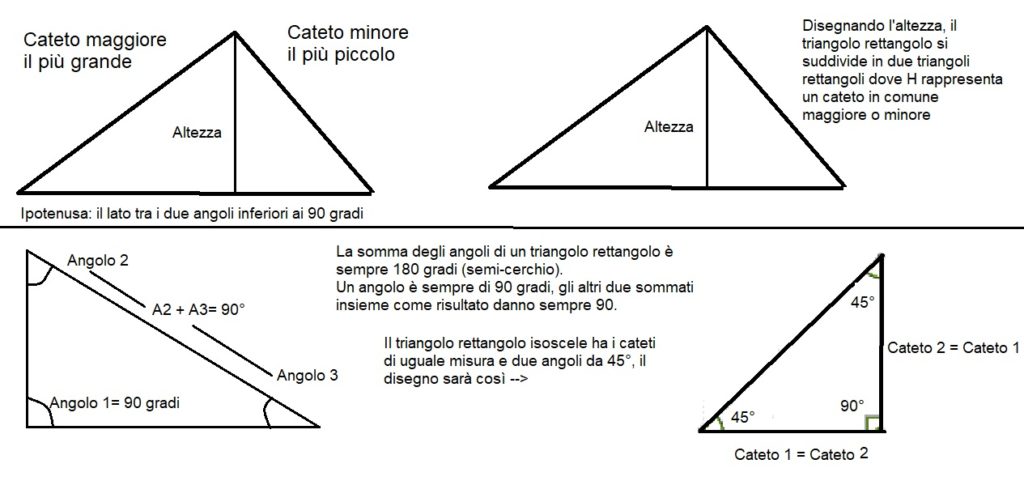
Il triangolo rettangolo è composto da tre lati, uno è chiamato ipotenusa e due sono chiamati b.

La definizione di ipotenusa è: lato opposto all’angolo retto.

La definizione di cateti invece è: i due lati adiacenti all’angolo retto. Il lato opposto all’angolo retto si chiama invece ipotenusa.

Ci sono tante proprietà da ricordare per questo particolare triangolo, abbiamo provato a sintetizzarle con un disegno. Ecco che cosa dovete ricordare

• Il triangolo rettangolo ha un angolo pari a 90 gradi
• Due lati sono perpendicolari tra di loro
• I due angoli inferiori a novanta gradi sono definiti acuti e complementari.
• La somma totale i tutti gli angoli del triangolo retto è 180 gradi.
• La somma degli angoli complementari è di 90 gradi anche se tra loro sono diversi.

Perimetro, formula principale e inverse

Il perimetro del Triangolo rettangolo si può calcolare con una semplice addizione. Da qui in avanti cateto maggiore avrà il simbolo c1, il cateto minore il simbolo c2

• ipotenusa + cateto maggiore (c1) + cateto minore o 2 (c2).

Ne deriva che l’ipotenusa si trova con questa sottrazione:

• perimetro totale – cateto 1 e cateto 2

Anche i singoli cateti si possono ricavare dalla sottrazione:

• perimetro – ipotenusa
• Perimetro – ipotenusa – cateto.

L’area del triangolo rettangolo si può trovare con due formule diverse.

Prima formula si basa sul semi-prodotto dei cateti quindi:

• Area = (Cateto 1 x Cateto 2) : 2

Seconda formula, basato sulla formula del rettangolo ma divisa per due

• Area = ipotenusa (considerata una base) x altezza (h) : 2

Quando si conosce l’area per trovare i singoli elementi del triangolo si possono fare operazioni inverse.

• C1= Area x 2 : c2
• C2= Area x 2 : c1
• Ipotenusa= area x 2 : altezza

L’altezza del triangolo rettangolo la troviamo con due formule

1. area x 2 : ipotenusa
2. cateto 1 x Cateto 2 : ipotenusa

Il teorema di Pitagora e il teorema di Euclide

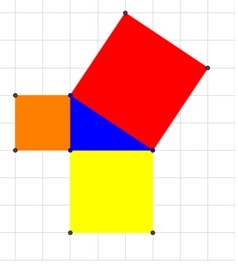
Pitagora e Euclide sono due matematici, filosofi e pensatori della Grecia Antica che hanno scritto dei teoremi sul triangolo rettangolo, ovvero degli enunciati dimostrabili con calcoli e disegni applicati sui lati, gli angoli e l’altezza. Dedicheremo un nuovo testo sul Teorema di Pitagora e i due di Euclide. Adesso è importante che memorizziate questa figura (fonte Wikipedia): su ogni lato è costruito un quadrato o un rettangolo.

Molto probabilmente ti sarà utile anche un ripasso alle formule degli altri triangoli: come il triangolo equilatero oppure il triangolo isoscele.