Triangolo isoscele: caratteristiche e formule

Se la geometria non è il tuo forte sei capitato nel posto giusto perché in questo articolo ti spiegheremo tutto quello che c’è da sapere sul triangolo isoscele.

Partiamo con il dirti che questa forma geometrica è formata da tre lati di cui due obliqui caratterizzati dalla stessa misura ed un altro lato chiamato anche base.

Partendo da questi elementi si può continuare a scoprire ancora molto sul triangolo isoscele: perimetro, area, altezza, ecc.

Ma procediamo con calma perché la geometria è una materia che necessita di ordine e precisione.

Triangolo isoscele: definizione e molto altro

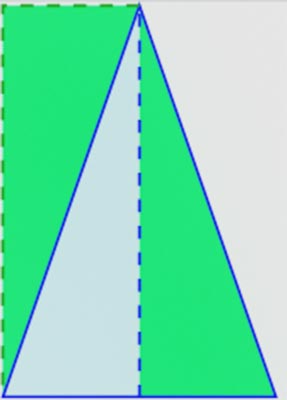
All’inizio di questo articolo abbiamo già scoperto cos’è un triangolo isoscele, ovvero è un triangolo con due lati di egual misura ed un lato diverso che fa da base.

Tra le tante cose da dire, la prima che devi sapere è che l’altezza disegnata al suo interno divide il triangolo in questione in due perfetti triangoli rettangoli.

Questo è un elemento importante da ricordare soprattutto nel momento in cui andremo a scoprire le diverse formule.

Ma come si calcola il perimetro? E l’area? Andiamo a scoprirlo in modo che tu possa risolvere qualsiasi tipo di problema tu ti trova davanti.

Quali sono le diverse formule del triangolo isoscele?

Le formule che devi sapere non sono poi tante, ma sono tutte estremamente importanti.

Ricordando che questo tipo di triangolo ha due lati uguali e che l’altezza lo divide in due triangoli rettangoli, troveremo le seguenti formule dirette:

• perimetro= (lato obliquo x 2) + base
• area= (base x altezza) : 2

Ci sono, poi, anche le formule inverse in base al perimetro:

• lato obliquo=(perimetro – base) : 2
• base= perimetro – (lato obliquo x 2)

Ed anche le formule inverse in base all’area:

• base= (area x 2) : altezza
• altezza= (area x 2) : base

Vi sono, poi, situazioni più complesse in cui magari non si hanno tutti i dati a disposizione ma si deve comunque arrivare ad una soluzione finale.

Ecco che qui torna ad essere utile la caratteristica citata in precedenza, ovvero l’altezza che divide il triangolo isoscele in due triangoli rettangoli.

Arriveremo, quindi, alle seguenti formule in cui spicca anche il Teorema di Pitagora:

• lato obliquo= √[ altezza² + (base:2)² ]
• altezza= √[ lato obliquo² + (base:2)² ]
• base= √( lato obliquo² – altezza² ) × 2