Triangolo equilatero: caratteristiche e formule

Il triangolo equilatero è una delle prime forme geometriche che si imparano tra i banchi di scuola e, tra l’altro, anche il più semplice da analizzare tra tutti i diversi triangoli.

Cominciamo con il dirti che, questo tipo di triangolo ha la caratteristica di avere tutti e tre i lati congruenti, ovvero di egual misura.

Durante la tua vita scolastica sicuramente ti capiterà di dover aver a che fare con questa forma geometrica e noi siamo qui proprio per aiutarti ad affrontarla e studiarla nel migliore dei modi.

Mettiti comodo e prendi appunti.

Triangolo equilatero: definizione e tutto quello che c’è da sapere

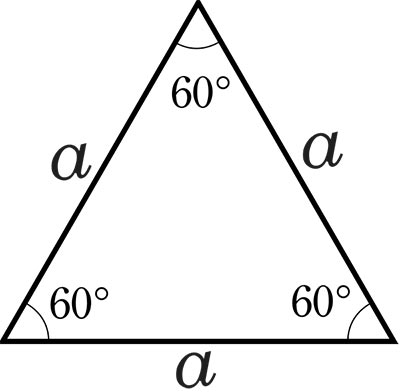
Quando si parla di un triangolo equilatero s’intende sempre un triangolo in cui i tre lati hanno esattamente la stessa misura.

Altra caratteristica importante, poi, è il fatto che al suo interno ha sempre e comunque tre angoli identici di 60°. Proprio per questo motivo viene anche chiamato con il termine di triangolo equiangolo.

Queste proprietà ti aiuteranno ad identificare immediatamente quando si tratta di un equilatero. Oltre ad aiutarti a disegnarlo anche in modo perfetto.

Ma passiamo, ora, ad esaminare anche le diverse formule per poter risolvere eventuali problemi e quiz matematici.

Quali sono le diverse formule del triangolo equilatero?

Le formule che riguardano questo tipo di triangolo sono davvero molto semplici sia da ricordare che da applicare.

Cominciamo con le principali formule dirette in assoluto:

• perimetro= lato x 3
• area= (base x altezza) : 2

Esistono, come anche per tutte le altre forme geometriche triangolari, delle formule inverse da poter usare in diversi casi:

• lato= perimetro : 3
• altezza= (area x 2) : base

Infine, ci sono delle situazioni particolari in cui si necessita di trovare una misura ma non si hanno tutti i diversi dati per utilizzare le formule prima citate. In questi casi si può utilizzare il Teorema di Pitagora:

• altezza= (lato x √ 3) : 2
• lato= (altezza x 2) : √ 3
• perimetro (conoscendo solo l’altezza)= (altezza x 2) x √ 3
• area (conoscendo solo il lato)= (√ 3 x 4) x lato²
• area (conoscendo solo l’altezza)= altezza² : √ 3