Rettangolo: formule e regole da conoscere

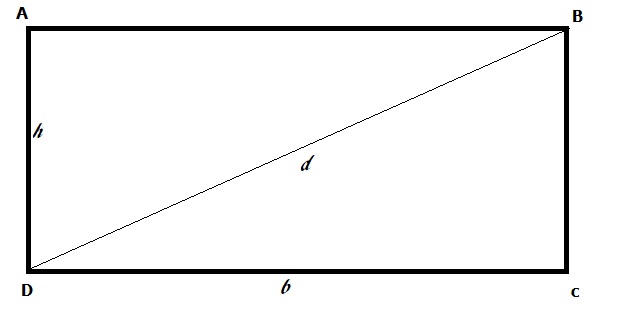
Abbiamo disegnato un rettangolo e denominato ogni angolo con una lettera.

• Il lato AD ma potrebbe anche essere BC è l’altezza e ho inserito come lettera h.
• AB o DC rappresentano le base e ho inserito come lettera la b.
• Infine, c’è la diagonale DB che sarà importante per studiare o ripassare il teorema di Pitagora, applicato ad un triangolo rettangolo.

Con questo disegno, ecco le principali caratteristiche e definizioni di questa figura piana.

Definizione e caratteristiche del rettangolo

Il rettangolo è un quadrilatero e un parallelogramma per via delle sue coppie di lati e i quattro angoli congruenti (stessa forma e dimensioni). Studiando questa figura si scopre che il quadrato può essere considerato un rettangolo per via dei sui angoli e dei quattro lati paralleli.

Gli angoli sono di 90 gradi e la diagonale divide il parallelogramma in due triangoli uguali, per questo motivo possono essere applicati i calcoli del Teorema di Pitagora per trovare la diagonale o risolvere altri problemi e quesiti.

Disegnando entrambe le diagonali si crea un punto definito centro del rettangolo. Inoltre si creano quattro triangoli isosceli uguali a coppie.

Studiando il cerchio e applicando le sue regole sui quadrilateri è importante conoscere questa caratteristica.

Le somme degli angoli opposti del rettangolo sono uguali. Per tale motivo, è sempre inscrivibile in una circonferenza il cui centro corrisponde a quello del quadrilatero

Inscrivibilità dei quadrilateri

Perimetro, area e diagonale del rettangolo

Il perimetro del rettangolo lo segneremo come P, può essere trovato con una semplice addizione oppure moltiplicazione e addizione.
Sarebbe, base moltiplicata per due più altezza moltiplicata per due

P= 2B + 2h

oppure guardando la figura

P= AB + BC + CD + DA

L’area si trova con una semplice moltiplicazione: Base per Altezza.

• A= b x h

I triangoli hanno la formula dell’area basata su questa moltiplicazione ma divisa per due. Con questa applicazione si riescono a risolvere molti problemi e quesiti geometrici.

Diagonale e Teorema di Pitagora

Infine, ecco come trovare la misura esatta della diagonale applicando il teorema di Pitagora. La regola dice che: in un triangolo rettangolo il quadrato costruito sull’ipotenusa è equivalente alla somma delle aree e dei quadrati costruiti sui cateti.

Nel rettangolo, la diagonale corrisponde all’ipotenusa dei due triangoli che costruisce. Quindi i lati base e altezza corrispondono ai cateti.

Conoscendo la base e l’altezza, il calcolo della diagonale si ottiene con la radice della somma del quadrato della base con il quadrato dell’altezza. La formula matematica è la seguente.