SoloScuola.com Appunti, riassunti, guide ed analisi per la scuola 
Il nostro argomento riguarda il prisma e le sue formule. Partiamo con il dire che il nostro testo analizzerà la forma retta e regolare, approfondirà con un capitolo a parte altre varianti di questo poliedro.
Le formule che studieremo e che vi saranno utili per risolvere problemi ed esercizi saranno: il volume, la superficie totale, di base e laterale considerando diversi elementi. Potremmo anche includere alcune formule di geometria piana come il perimetro e l’area del rettangolo, sicuramente sarà una buona occasione per ripassarle.
Volume del prisma, formule dirette e indirette
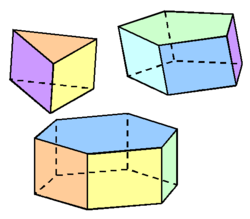
Il prisma è un poliedro formato da due poligoni chiamati basi e tanti lati quanti ne hanno le basi.
I lati sono tutti parallelogrammi. Un parallelepipedo si può definire un prisma composto da 6 parallelogrammi e può essere rettangolo quadrato. Ecco alcuni esempi di prisma trovati sul web.
Il volume nella geometria solida indica lo spazio occupato da un corpo, si usa sempre il m³ (metro cubo) come unità per i calcoli.
Per studiare tutte le formule del prisma partiremo dal suo volume: prodotto dell’area di una delle sua basi per la distanza tra i piani ai quali appartengono. Questa distanza si può definire anche altezza, nel prisma retto corrisponde alla lunghezza di uno spigolo.
Le formule matematiche dirette e indirette sono le seguenti.
V= Sb x h
SB= V : H
H= V/Sb
- V= Volume
- Sb= superficie di base
- H= altezza.
Superficie di base e superficie laterale, altre formule del prisma
La superficie totale di un prisma è composta dalla superficie di base e dalla superficie laterale. Ecco i simboli che useremo Stot, Sbase e Slat.
La superficie di base corrisponde alla formula di uno solo dei poligoni di base.
La superficie laterale è invece la somma di tutte le facce che dipende sempre dal numero dei lati dei due poligoni.
Le formule per trovare la superficie totale, di base e laterale sono le seguenti.
Stot = Slat + 2Sb
Slat = Stot – 2Sb
Sb= Stot-Slat/2
La superficie laterale di un prisma retto può essere trovato anche con questa formula.
- SLat = 2P x h ovvero perimetro di base per altezza.
