SoloScuola.com Appunti, riassunti, guide ed analisi per la scuola 
Il cubo ha molte formule da studiare, le vedremo nel seguente articolo e approfondiremo gli aspetti più importanti.
Il cubo si chiama anche esaedro regolare e rientra in una categoria di solidi definiti platonici. E’ composto da:
- 6 facce quadrate, 8 vertici e 12 spigoli.
In ogni vertice si incontrano tre spigoli e si intersecano tre facce. Spigoli e facce a due a due si definiscono ortogonali. Il cubo rientra tra i parallelepipedi retti e regolari, tra i prismi quadrati e trapezoedri. Da qui partiamo con il suo lungo elenco di formule. Per questo testo è importante ripassare il quadrato come figura piana.
Il disegno del cubo, la diagonale e il suo sviluppo
Prima di considerare le formule è importante studiare il disegno del cubo. L’esaedro ha quattro diagonali congruenti e sono importanti per risolvere problemi e quesiti.
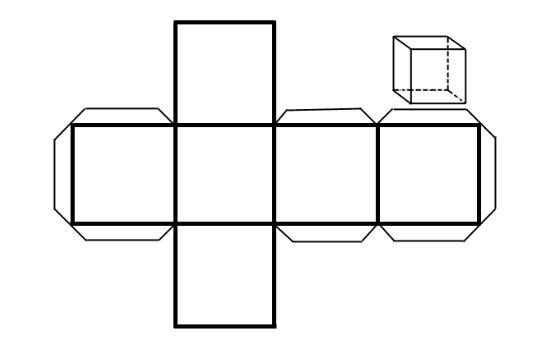
La definizione di diagonale del cubo è: segmento che unisce due suoi vertici non appartenenti alla stessa faccia. Il secondo disegno che mostra lo sviluppo di un cubo lo potete utilizzare per realizzare un modello in cartone.
Cubo: formule del volume e della diagonale
Le prime formule del cubo dirette e indirette che studiamo sono del volume. Scopriamo lo spazio occupato dal cubo. Si calcola quindi un lato elevato alla terza.
V= L³
L’operazione inversa per trovare il lato e quindi parte della superficie è una radice cubica.
L= ³√volume (radice cubica del volume).
La radice cubica e non è usata anche per calcolare la diagonale.
- D = L √3.
- L = D/ √3
Superfici del cubo, formule dirette e indirette
Studiamo la superficie del cubo considerando le formule principali dirette e indirette.
La superficie totale del cubo può essere trovata in due modi. Con un’addizione e un potenza al quadrato.
- Superficie totale (Stot) = superficie laterale più il doppio della superficie di base.
- Stot= Slat + 2Sbase
Oppure conoscendo uno spigolo si può calcolare considerando sei volte il lato al quadrato.
- Stot = 6L².
Se si ha la diagonale, si otterrà il risultato con il doppio del quadrato della diagonale.
- Stot = 2D²
La superficie laterale del cubo si ottiene con una semplice sottrazione, totale meno i due quadrati di base.
- Slat = Stot – 2 Sbase
La superficie di base del cubo si ha con una formula inversa.
- Sbase = Stot – Slat / 2
