Trapezio rettangolo: caratteristiche e formule

Il trapezio rettangolo è una forma geometrica che spesso può mettere in crisi diversi studenti.

La verità, però, è che se la analizzi con attenzione potresti scoprire che non è poi così complicata come credi.

Partiamo subito con il dirti che il trapezio rettangolo fa parte della famiglia dei trapezi.

Viene definito rettangolo per la sua tipica caratteristica dell’avere un angolo retto, ovvero di 90°.

Ma andiamo a conoscere un po’ meglio questa forma geometrica.

Trapezio rettangolo: definizione e tutto quello che c’è da sapere

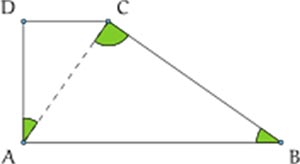
Il trapezio rettangolo è un quadrilatero in cui sono presenti due lati paralleli ed altri due lati di cui uno è obliquo.

I due lati paralleli sono chiamati anche con il nome di basi: base minore e base maggiore.

Il lato perpendicolare alle base, poi, è quello che va a formare il tipico angolo retto che dà anche il nome a questo tipo di trapezio.

Lungo la tua carriera scolastica sicuramente ti capiterà di trovarti davanti un trapezio rettangolo e di dover anche calcolarne le diverse misure.

Tranquillo, ci siamo qui noi ad aiutarti.

Quali sono le diverse formule del trapezio rettangolo?

Per risolvere i diversi problemi sul trapezio rettangolo si utilizzano le formule generiche di tutti i trapezi.

Questo ti agevola di gran lunga perché ti permette di poter gestire le diverse tipologie di trapezi senza andare in confusione e commettere errori.

Ma quali sono queste formule?

Cominciamo con le formule dirette:

• perimetro= base minore+base maggiore+altezza+lato obliquo
• area= [(base minore+base maggiore) x altezza] : 2

Procediamo, ora, con le formule inverse che possono esserti molto utili in diversi casi. Per alcune sarà necessario applicare anche il Teorema di Pitagora:

• base maggiore (conoscendo il perimetro)= perimetro-base minore-lato obliquo-altezza
• base maggiore (conoscendo l’area)= [(2xarea) : altezza] – base minore
• base minore (conoscendo il perimetro)= perimetro-base maggiore-lato obliquo-altezza
• base minore (conoscendo l’area)= [(2xarea) : altezza] – base maggiore
• lato obliquo (conoscendo il perimetro)= perimetro-base minore-base maggiore-altezza
• lato obliquo (conoscendo solo basi ed altezza)= √ altezza² + (base maggiore-base minore)²
• altezza (conoscendo il perimetro)= perimetro-base minore-base maggiore-lato obliquo
• altezza (conoscendo l’area)= (2xarea) : (base maggiore+base minore)
• altezza (conoscendo solo basi e lato obliquo)= √ lato obliquo² – (base maggiore-base minore)²

Se ti occorrono le formule del trapezio scaleno e del trapezio isoscele leggi i nostri articoli.