Pentagono formule di base:
- Perimetro considerando il lato
- come trovare il lato con formula inversa
- area del pentagono con l’apotema
- calcolo inverso per trovare apotema o perimetro.
Per pentagono si intende un poligono composto da cinque lati uguali, cinque vertici e cinque angoli di 108°, sono tutti uguali. Ecco che cosa studieremo in questo testo.
Lo studio delle formule base di un pentagono dirette o inverse devono essere approfondite con altri calcoli e regole più complesse. Ad esempio, considerando un pentagono iscritto in una circonferenza e altre caratteristiche.
Tutto ciò che è descritto qui non può essere sempre applicato ad un pentagono irregolare. Per questo caso il poligono si suddivide in più figure geometriche.
Perimetro del pentagono, formule dirette e inverse con regole
In questo nuovo appunto di matematica consideriamo un pentagono regolare semplice.
Quindi è un poligono equilatero ed equiangolo, convesso per i suoi angoli inferiori a 180 gradi. Equo significa uguale, quindi uguale lati e uguali angoli. Come tutti i poligoni con queste caratteristiche si può inscrivere dentro ad un cerchio per estrapolare altre formule e regole più complesse.
Il perimetro di un pentagono si trova con una semplice moltiplicazione: un lato per cinque.
- 2p significa perimetro
- L significa lato.
2P = 5L
La formula inversa per trovare il lato con il perimetro è una semplice divisione.
L = 2P/5 vuol dire perimetro diviso cinque.
Ci sono formule del pentagono interessanti per calcolare il lato considerando la misura dell’apotema e il numero fisso che tutti i poligoni regolari hanno. Per il pentagono è: 0,688.
Calcolare l’area del pentagono e le sue formule indirette.
L’area del pentagono si può trovare con tre formule:
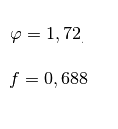
- conoscendo l’apotema, useremo la lettera Ap
- se si conosce il numero fisso del pentagono che è 0,688, useremo la lettere F
- conoscendo la costante dell’area che è 1,72. Ha un simbolo speciale come potete vedere nella figura accanto. Qui dal computer useremo CAr
- Conoscendo l’apotema del pentagono, si può calcolare l’area con una semplice operazione.
Area = (Perimetro x Apotema)/2
Se abbiamo l’area e l’apotema, per scoprire il perimetro dovremo fare questo calcolo, diviso per cinque si ottiene un lato.
Perimetro = (Apotema * 2) / area
Con la costante, che abbiamo detto ha valore di 1,72, l’area del pentagono regolare si calcola così.
- Quadrato del lato per costante, ovvero, 1,72.
Area = Lato² x 1,72 (C.area)
Con il numero fisso che vale 0,688 l’area si calcola così. Quadrato del lato per cinque per 0,688 il tutto diviso due.
A= (5L²x F) / 2
Se si hanno come valori conosciuti apotema e numero fisso, il calcolo avverrà con questa divisione.
- Apotema alla seconda per cinque, il tutto diviso per il numero fisso moltiplicato per 2.
A = (5a²) / 2F
 SoloScuola.com Appunti, riassunti, guide ed analisi per la scuola
SoloScuola.com Appunti, riassunti, guide ed analisi per la scuola 





